Поиск
| Автор | Сообщение |
|---|---|
|
Екатерина
#
26 июн 2006 |
|
|
О.А.
#
26 июн 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
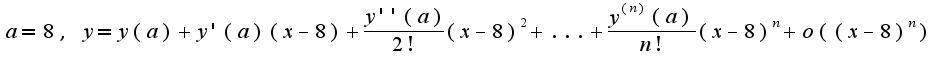 Затем найти четыре производных от данной функции и посчитать найденные производные в точке
Затем найти четыре производных от данной функции и посчитать найденные производные в точке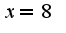
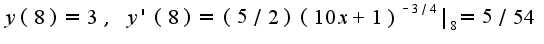 и т.д.
и т.д.