Поиск
| Автор | Сообщение |
|---|---|
|
Владислав
#
5 окт 2014 Владислав
9 окт 2014
|
|
|
o_a
#
5 окт 2014 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
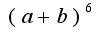 её нужно разложить как в школе обычные формулы сокращенного умножения биноминальные коэффициенты через обычные числа
вот так:
её нужно разложить как в школе обычные формулы сокращенного умножения биноминальные коэффициенты через обычные числа
вот так: 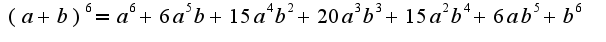 или в виде больших букв С?
Я еще начал делать самую первую дз, по теории множеств.
Но на фото, где дз плохо видны первый и четвертый номера можете,пожалуйста, сказать условия 1 и 4 задачи.
или в виде больших букв С?
Я еще начал делать самую первую дз, по теории множеств.
Но на фото, где дз плохо видны первый и четвертый номера можете,пожалуйста, сказать условия 1 и 4 задачи.
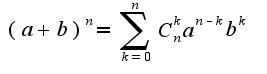 , где
, где 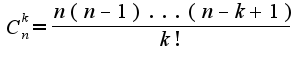 Теперь ее надо применить для конкретного примера
Теперь ее надо применить для конкретного примера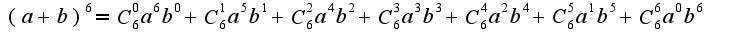 Если в этой формуле посчитать все
Если в этой формуле посчитать все 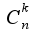 , то получится написанная вами формула, например,
, то получится написанная вами формула, например, 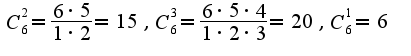 На доске написано: существуют ли множества такие
На доске написано: существуют ли множества такие , которые удовлетворяют условиям
, которые удовлетворяют условиям 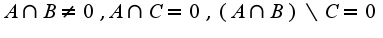 Тема занятия в пятницу- техника вычисления пределов. На дом решить из Кудрявцева Л.Д. 8.18(13,12),8.25(9,10), 8.27(12)Б8.28(9,10), 8.32(1), 8.34(3,5),8.95(8,9),8.124(5,4)
Тема занятия в пятницу- техника вычисления пределов. На дом решить из Кудрявцева Л.Д. 8.18(13,12),8.25(9,10), 8.27(12)Б8.28(9,10), 8.32(1), 8.34(3,5),8.95(8,9),8.124(5,4)