Поиск
| Автор | Сообщение |
|---|---|
|
М.В
#
9 дек 2005 |
|
|
О.А.
#
9 дек 2005 |
|
|
......
#
17 дек 2005 |
|
|
О.А.
#
17 дек 2005 |
|
|
......
#
17 дек 2005 |
|
|
ирина
#
17 июн 2006 |
|
|
О.А.
#
17 июн 2006 |
|
|
ната
#
18 июн 2006 |
|
|
Карина
#
18 июн 2006 |
|
|
Карина
#
18 июн 2006 |
|
|
О.А.
#
19 июн 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
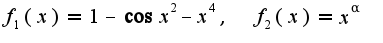 при
при 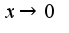 . Предел должен быть равен постоянной, отличной от нуля, степень
. Предел должен быть равен постоянной, отличной от нуля, степень 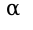 и будет порядком.
и будет порядком.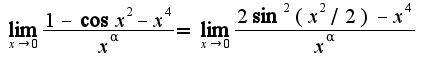 Используя первый замечательный предел
Используя первый замечательный предел 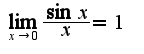 , получим
, получим 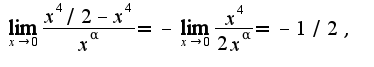 если
если 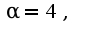 т.е. порядок равен 4.
т.е. порядок равен 4.
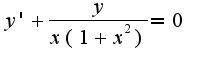 Данное уравнение -с разделяющимися переменными:
Данное уравнение -с разделяющимися переменными: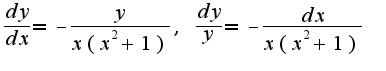
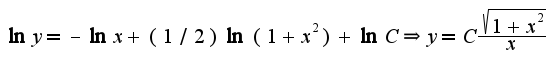 2)Затем используют метод вариации произвольной константы C,т.е. подставляют в уравнение найденное решение, считая, что C(x)зависит от x.Легко найти
2)Затем используют метод вариации произвольной константы C,т.е. подставляют в уравнение найденное решение, считая, что C(x)зависит от x.Легко найти 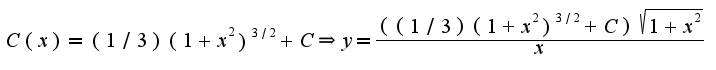
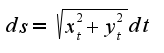 Сл-но,
Сл-но, 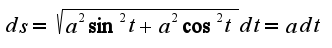 Тогда
Тогда