По формуле тейлора

Форумы > Консультация по матанализу > По формуле тейлора

Автор	Сообщение
Тёмная_Личность # 6 янв 2006	Уважаемая, Ольга Александравна не пможете ли вы мне вот с таким примерчиком, вот уж совсем не поимаю как делать,а экзамен скоро((( Извините, что не в ЛаТехе ибо я его ещё не освоил доконца надеюсь поймёте сию запись Lim(sin(x)/x)^ctg^2(7x) при x --> 0, Заранее спасибо! =) p.s.// написано что нужо сие вычислить с помощью формулы Тейлора.
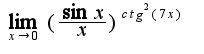О.А. # 7 янв 2006	$\lim_{x\rightarrow 0}(\frac{\sin x}{x})^{ctg^2(7x)}$ Известны разложения по формуле Тейлора при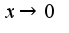 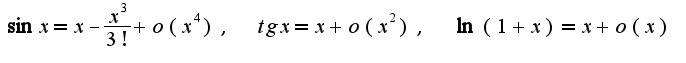$x\rightarrow 0$ $\sin x=x-\frac{x^3}{3!}+o(x^4),\;\;tg x=x+o(x^2),\;\;\ln(1+x)=x+o(x)$ Для вычисления предела используем данные разложения,предварительно прологарифмируем подпредельное выражение: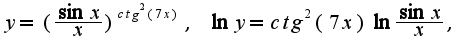 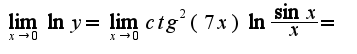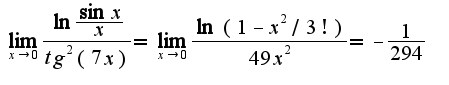$y=(\frac{\sin x}{x})^{ctg^2(7x)},\;\ln y=ctg^2(7x)\ln \frac{\sin x}{x},$ $\lim_{x\rightarrow 0}\ln y=\lim_{x\rightarrow 0}ctg^2(7x)\ln \frac{\sin x}{x}=$ $\lim_{x\rightarrow 0}\frac{\ln \frac{\sin x}{x}}{tg^2(7x)}=\lim_{x\rightarrow 0}\frac{\ln(1-x^2/3!)}{49x^2}=-\frac{1}{294}$ Но т.к. находили предел логарифма от 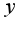$y$ , то переходя к пределу y, получим, что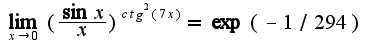 $\lim_{x\rightarrow 0}(\frac{\sin x}{x})^{ctg^2(7x)}=\exp(-1/294)$
Тёмная_Личность # 7 янв 2006	Огромнейшее вам спасибо!!! вы так меня спасли!!! Теперь я хоть приблизительно понял, как по формуле Тейлора можо функцию раскладавать, а то никак она не давалась... конечно всё-таки интересно почему у синуса добавачный член именно o(x^4)...именно в доб. члене я совсем путаюсь, ничего не посоветуете, ещё раз Вам, Ольга Александровна спасибо!!!
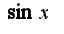О.А. # 7 янв 2006	При разложении функции $\sin x$ по формуле Тейлора надо учитывать, что слагаемые с четными номерами равны нулю, в силу обращения в нуль производных в точке 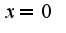$x=0$ , поэтому остаточный член, записанный в форме Пеано есть бесконечно малая функция по сравнению со следующим слагаемым. 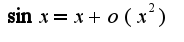$\sin x=x+o(x^2)$ Однако, многочлен 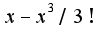$x-x^3/3!$ является многочленом Тейлора как третьего, так и четвертого порядков функции $\sin x$ в нулевой точке. Поэтому при вычислении пределов полезно оценить заранее, какого порядка малости погрешность не влияет на предел.
Тёмная_Личность # 7 янв 2006	Спасибо, Вам, Ольга Александровна!
Роман # 4 дек 2006	Спасибо, Ольга Александровна! Мне вы тоже помогли :)
Ваш ответ:	Чтобы написать сообщение, необходимо войти или зарегистрироваться

Форумы > Консультация по матанализу > По формуле тейлора

Чтобы написать сообщение, необходимо войти или зарегистрироваться