Поиск
| Автор | Сообщение |
|---|---|
|
Сергей
#
22 ноя 2007 |
|
|
Сергей
#
22 ноя 2007 |
|
|
О.А.
#
22 ноя 2007 |
|
|
Сергей
#
22 ноя 2007 |
|
|
О.А.
#
22 ноя 2007 |
|
|
Сергей
#
23 ноя 2007 |
|
|
О.А.
#
23 ноя 2007 |
|
|
Сергей
#
23 ноя 2007 |
|
|
О.А.
#
23 ноя 2007 |
|
|
Сергей
#
23 ноя 2007 |
|
|
О.А.
#
23 ноя 2007 |
|
|
Сергей
#
24 ноя 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
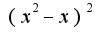 , но от этого суть решения не меняется. К нулю мы приравниваем числитель, что я собственно и сделал(а пояснить - забыл). А вот как решить это уравнение - не понимаю. Пробовал делать замену
, но от этого суть решения не меняется. К нулю мы приравниваем числитель, что я собственно и сделал(а пояснить - забыл). А вот как решить это уравнение - не понимаю. Пробовал делать замену 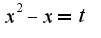 , пришел к уравнению:
, пришел к уравнению:
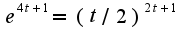 Что делать дальше - не знаю.
Пробовал решать в MathCADe. Получаются два "странных" корня x:
-3.3127... и 4.3127...
Что делать дальше - не знаю.
Пробовал решать в MathCADe. Получаются два "странных" корня x:
-3.3127... и 4.3127...
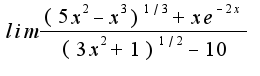 у меня получается
у меня получается 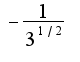 Это правильный ответ? (MathCAD выдает
Это правильный ответ? (MathCAD выдает 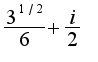 )
Заранее спасибо!
)
Заранее спасибо!
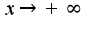 правильный
правильный
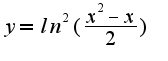 Ее область определения:
Ее область определения: 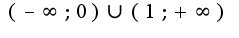 Находим предел функции в
Находим предел функции в 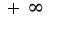 :
:
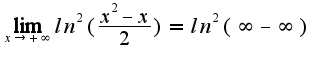 Вопрос. Как раскрыть эту неопределенность?
Или можно воспользоваться теоремой о сумме бесконечно больших и записать:
Вопрос. Как раскрыть эту неопределенность?
Или можно воспользоваться теоремой о сумме бесконечно больших и записать:
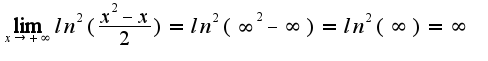 ?
?
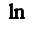 является непрерывной, то можно поменять местами знак предела и логарифма, поэтому более корректной будет запись
является непрерывной, то можно поменять местами знак предела и логарифма, поэтому более корректной будет запись
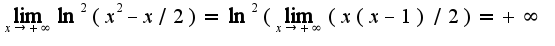
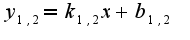 имеем:
имеем:
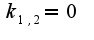
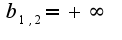 Это означает, что наклонных асимптот не существует, верно?
Это означает, что наклонных асимптот не существует, верно?