Поиск
| Автор | Сообщение |
|---|---|
|
Вера
#
11 ноя 2007 |
|
|
Вера
#
12 ноя 2007 |
|
|
Вера
#
12 ноя 2007 |
|
|
О.А.
#
12 ноя 2007 |
|
|
Вера
#
12 ноя 2007 |
|
|
Вера
#
12 ноя 2007 |
|
|
О.А.
#
12 ноя 2007 |
|
|
Вера
#
12 ноя 2007 |
|
|
О.А.
#
12 ноя 2007 |
|
|
Вера
#
12 ноя 2007 |
|
|
О.А.
#
13 ноя 2007 |
|
|
Линк
#
28 сен 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
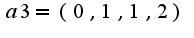 ,
, 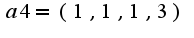 ,
, 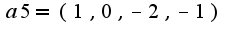 ,
, 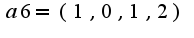 .
Необходимо дополнить линейно независимую часть а1, а2 до базиса системы а1,а2,а3,а4,а5,а6 и все векторы, не вошедшие в базис, разложить по базису
.
Необходимо дополнить линейно независимую часть а1, а2 до базиса системы а1,а2,а3,а4,а5,а6 и все векторы, не вошедшие в базис, разложить по базису 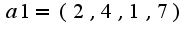 ,
, 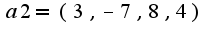 Решение:
Если часть а1, а2 линейно независима, то К1*а1 + К2*а2 =0 лишь в случае К1=К2=0. Эти вектора некомпланарны.
Можем записать: 2*К1*i+4*K1*j+1*K1*k+7*К1*m + 3*K2*i-7*K2*i+8*K2*k-4*K2*m=0
Так здесь пространство четырехмерное, то я к трем единичным ортам "i,j,k" добавила четвертую "m".
А что дальше делать? Записать условие перпендикулярности?
Подскажите, пожалуйста!
Решение:
Если часть а1, а2 линейно независима, то К1*а1 + К2*а2 =0 лишь в случае К1=К2=0. Эти вектора некомпланарны.
Можем записать: 2*К1*i+4*K1*j+1*K1*k+7*К1*m + 3*K2*i-7*K2*i+8*K2*k-4*K2*m=0
Так здесь пространство четырехмерное, то я к трем единичным ортам "i,j,k" добавила четвертую "m".
А что дальше делать? Записать условие перпендикулярности?
Подскажите, пожалуйста!