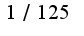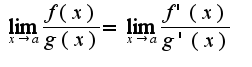Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Поиск| Автор | Сообщение |
|---|---|
|
Вадим
#
15 окт 2007 |
|
|
О.А.
#
15 окт 2007 |
|
|
Константин Ш.
#
5 янв 2008 |
|
|
О.А.
#
5 янв 2008 |
|
|
Константин Ш.
#
6 янв 2008 |
|
|
Костя
#
26 янв 2008 |
|
|
Оля
#
19 мар 2008 |
|
|
О.А.
#
19 мар 2008 |
|
|
Lim
#
21 окт 2008 |
|
|
Den
#
30 ноя 2008 |
|
|
О.А.
#
30 ноя 2008 |
|
|
Александра
#
30 ноя 2008 |
|
|
О.А.
#
1 дек 2008 |
|
|
Александра
#
1 дек 2008 |
|
|
О.А.
#
1 дек 2008 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
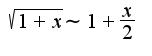 при
при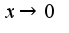
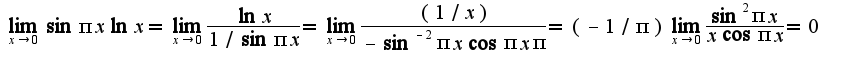
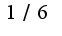
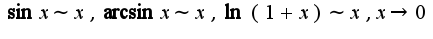 предварительно прологарифмируйте,затем используйте указанную эквивалентность функций, ответ
предварительно прологарифмируйте,затем используйте указанную эквивалентность функций, ответ