Поиск
| Автор | Сообщение |
|---|---|
|
Лим Д
#
14 дек 2011 |
|
|
o_a
#
14 дек 2011 |
|
|
paulinio
#
18 дек 2011 |
|
|
o_a
#
18 дек 2011 |
|
|
paulinio
#
18 дек 2011 |
|
|
o_a
#
18 дек 2011 |
|
|
paulinio
#
19 дек 2011 |
|
|
o_a
#
19 дек 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
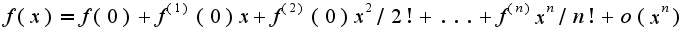 Для разложения по формуле данных функций можно воспользоваться готовыми разложениями
1)
Для разложения по формуле данных функций можно воспользоваться готовыми разложениями
1) 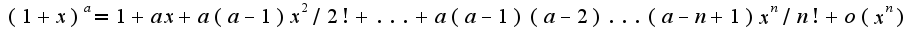 2)
2)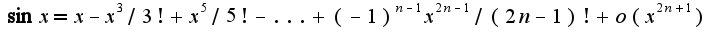
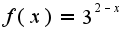
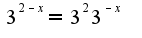 и затем использовать разложение для
и затем использовать разложение для 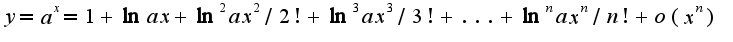
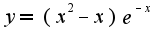 , то надо разложить
, то надо разложить 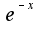 по формуле Маклорена, затем умножить каждое слагаемое на
по формуле Маклорена, затем умножить каждое слагаемое на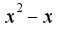 и привести подобные
Для решения номера 18.2 6
и привести подобные
Для решения номера 18.2 6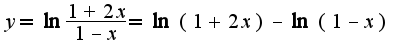 записать разложения для функции логарифм, затем привести подобные, напоминаю, что
записать разложения для функции логарифм, затем привести подобные, напоминаю, что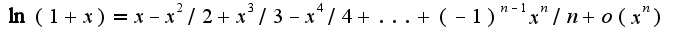
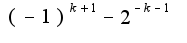
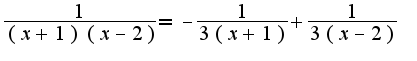 , затем каждое из слагаемых разложить по формуле Маклорена и привести подобные
, затем каждое из слагаемых разложить по формуле Маклорена и привести подобные