Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
О.А.
#
6 ноя 2005 |
|
|
О.А.
#
6 ноя 2005 |
|
|
Xman
#
12 ноя 2005 |
|
|
О.А.
#
12 ноя 2005 |
|
|
Любопытный человек
#
14 ноя 2005 |
|
|
О.А.
#
14 ноя 2005 |
|
|
Xman
#
14 ноя 2005 |
|
|
О.А.
#
15 ноя 2005 |
|
|
Я
#
15 ноя 2005 |
|
|
О.А.
#
15 ноя 2005 |
|
|
Я
#
15 ноя 2005 |
|
|
Прохор
#
16 ноя 2005 |
|
|
О.А.
#
16 ноя 2005 |
|
|
Прохор
#
17 ноя 2005 |
|
|
Прохор
#
17 ноя 2005 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
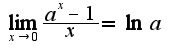 можно, используя замену переменной
можно, используя замену переменной 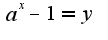 , а затем использовать выражение
, а затем использовать выражение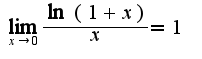 . Чтобы перейти к нужному основанию логарифма, можно использовать формулу
. Чтобы перейти к нужному основанию логарифма, можно использовать формулу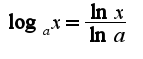
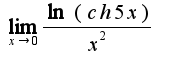 , надо использовать равенство
, надо использовать равенство 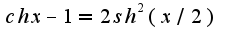
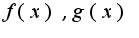 определены и дифференцируемы в некоторой окр-ти т.a,
определены и дифференцируемы в некоторой окр-ти т.a, 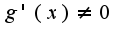 в данной окрестности,
в данной окрестности, 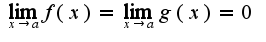 .Тогда если существует предел
.Тогда если существует предел 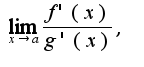 то существует
то существует 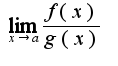 Причем справедливо равенство
Причем справедливо равенство 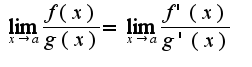
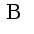 , если
, если 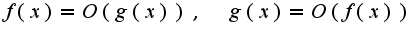 Сл-но,
Сл-но, 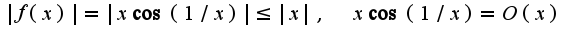 при
при 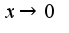 Но, обратное неравенство не выполняется(т.е
Но, обратное неравенство не выполняется(т.е 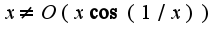 ), поэтому данные функции не являются функциями одного порядка.
), поэтому данные функции не являются функциями одного порядка.
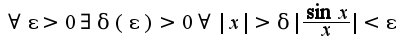 Учитывая, что функция
Учитывая, что функция 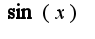 ограничена сверху единицей, получим
ограничена сверху единицей, получим 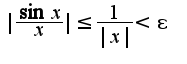 Т.о. получаем зависимость между
Т.о. получаем зависимость между 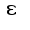 и
и 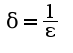 , Поэтому
, Поэтому 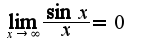 Данный факт еще и объясняется свойствами бесконечно малых функций: произведение б.м.функции на ограниченную равно б.м.
Данный факт еще и объясняется свойствами бесконечно малых функций: произведение б.м.функции на ограниченную равно б.м.