Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
О.А.
#
12 янв 2006 |
|
|
Инкогнито
#
14 янв 2006 |
|
|
О.А.
#
14 янв 2006 |
|
|
Математик
#
14 янв 2006 |
|
|
О.А.
#
14 янв 2006 |
|
|
Зачем_мне_ник
#
15 янв 2006 |
|
|
О.А.
#
15 янв 2006 |
|
|
Зачем_мне_ник
#
16 янв 2006 |
|
|
О.А.
#
16 янв 2006 |
|
|
Математик
#
16 янв 2006 |
|
|
О.А.
#
16 янв 2006 |
|
|
Лагранженко
#
17 янв 2006 |
|
|
Алексей
#
25 янв 2006 |
|
|
О.А.
#
25 янв 2006 |
|
|
Алексей
#
25 янв 2006 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
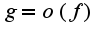 по базе
по базе  , то тем более
, то тем более 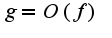 по базе
по базе 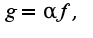 где
где 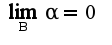 .Сл-но,
.Сл-но, 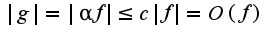 , т.к.
, т.к. 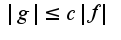 по указанной базе.Например,
по указанной базе.Например, 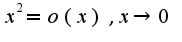 , но и
, но и 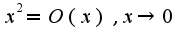
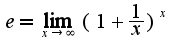 Еще раз напишите условие примера, а то неясно, какой надо найти предел.
Еще раз напишите условие примера, а то неясно, какой надо найти предел.