Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
О.А.
#
16 апр 2006 |
|
|
errant
#
16 апр 2006 |
|
|
О.А.
#
16 апр 2006 |
|
|
Chelovek
#
28 апр 2006 |
|
|
errant
#
28 апр 2006 |
|
|
О.А.
#
28 апр 2006 |
|
|
Зачем_мне_ник
#
28 мая 2006 |
|
|
О.А.
#
28 мая 2006 |
|
|
САБ
#
28 мая 2006 |
|
|
nonick
#
28 мая 2006 |
|
|
О.А.
#
28 мая 2006 |
|
|
О.А.
#
28 мая 2006 |
|
|
Зачем_мне_ник
#
2 июн 2006 |
|
|
О.А.
#
2 июн 2006 |
|
|
Chelovek
#
3 июн 2006 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
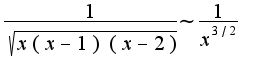 при
при 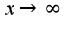 И т.к.
И т.к. 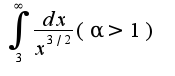 -сходится, то сходится и исходный интеграл.
-сходится, то сходится и исходный интеграл.
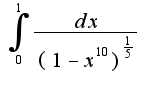 иследовать на сходимость.
иследовать на сходимость.
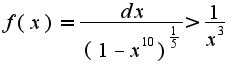 ,а интеграл
,а интеграл 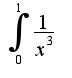 - расходящийся поэтому расходящийся исходный интеграл ?
- расходящийся поэтому расходящийся исходный интеграл ?
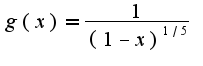 Поэтому интеграл сходится, т.к.
Поэтому интеграл сходится, т.к. 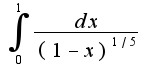 -сходится,
-сходится, 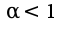
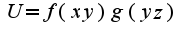 , найти
, найти 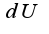
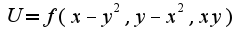 Найти
Найти 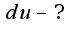
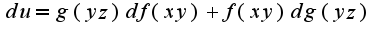 ,где
,где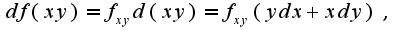
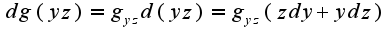 Сл-но,
Сл-но, 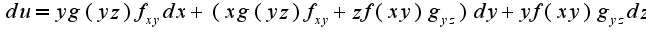 2)
2)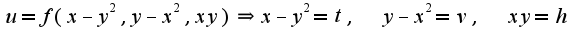
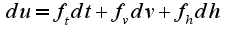
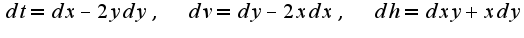 Затем надо все найденные дифференциалы подставитьв
Затем надо все найденные дифференциалы подставитьв 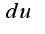 и привести подобные при
и привести подобные при 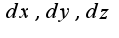
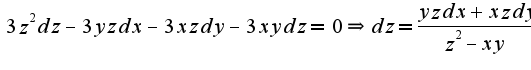 Дифференцируем уравнение еще раз:
Дифференцируем уравнение еще раз: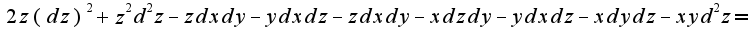
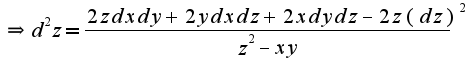
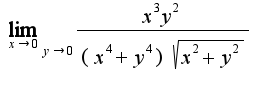
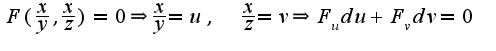
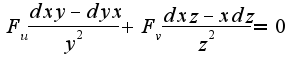 Отсюда находим
Отсюда находим 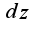
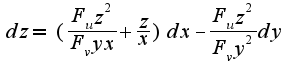 Ясно, что из выражения для dz легко найти
Ясно, что из выражения для dz легко найти 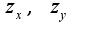 -которые являются коэффициентами при dx,dy,
-которые являются коэффициентами при dx,dy,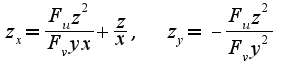 и подставляя найденные частные производные в уравнение
и подставляя найденные частные производные в уравнение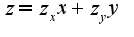 , получим тождество.
, получим тождество.