Поиск
Константин
#
5 ноя 2007
|
В методичке написано, что главная часть и порядок малости(роста) находятся пределом отношения двух функций f(x)/g(x) в моём случае это
f(x)=(x-2)/((x)^(5)+1)(x в пятой)
g(x)=(2+sinx)/(x)^(3)(x в кубе) этот предел равен нулю.Что делать?ОбЪясните, пожалуйста!!!
Если можно ещё один вопрос:
Найти точки разрыва функции f(x) и определить их характер.
f(x)={ (sqrt(x)-2)/((x)^(2)-4x),x>0
{ (e)^(-1/x), x<0
Ещё раз спасибо!!!!!!!!!!
|
Анатолий
#
5 ноя 2007
|
А, прошу прощения. Я думал, что нужно найти порядок малости относительно функции 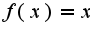 . В общем случае:
если существует 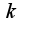 , такое, что 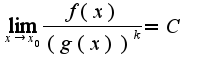 не равное 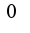 , то говорят, что 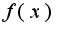 есть бесконечно малая порядка 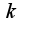 , относительно g(x).
Итак, какой у Вас вопрос?
Найти порядок малости какой функции относительно какой?
|
Константин
#
5 ноя 2007
|
Если честно, я не знаю.Звучит так:
б)для каждой функции f и g записать главную часть при х->беск., указать их порядки малости(роста)
f(x)=(x-2)/((x)^(5)+1)(x в пятой)
g(x)=(2+sinx)/(x)^(3)(x в кубе)
Если делать в общем случае, то С=0 и что делать?Если относительно х,то
как найти lim g(x)/(x)^(r)
Не могли бы вы подсказать с другим вопросом:
Найти точки разрыва функции f(x) и определить их характер.
f(x)={ (sqrt(x)-2)/((x)^(2)-4x),x>0
{ (e)^(-1/x), x<0
Для удобства можно ли с Вами связаться, например в ICQ или Агенте?
Ещё раз спасибо!!!!!!!!!!!
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
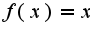 . В общем случае:
если существует
. В общем случае:
если существует 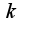 , такое, что
, такое, что 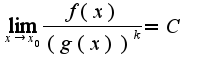 не равное
не равное 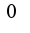 , то говорят, что
, то говорят, что 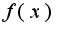 есть бесконечно малая порядка
есть бесконечно малая порядка