Поиск
| Автор | Сообщение |
|---|---|
|
o_a
#
21 мар 2020 o_a
24 мар 2020
|
|
|
o_a
#
24 мар 2020 o_a
24 мар 2020
|
|
|
o_a
#
24 мар 2020 o_a
24 мар 2020
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
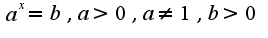
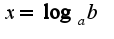 То есть, логарифмом называется показатель степени, в который надо возвести число
То есть, логарифмом называется показатель степени, в который надо возвести число 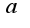 , чтобы получить
, чтобы получить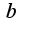 2)основное логарифмическое тождество
2)основное логарифмическое тождество 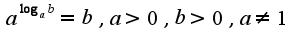 Примеры:
Примеры: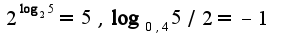 3)Свойства логарифмов:
3)Свойства логарифмов:
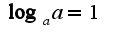
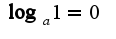
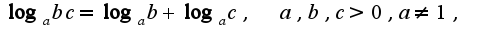
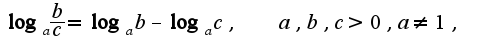
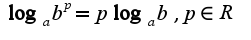
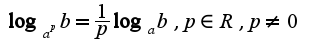
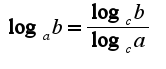 График логарифмической функции
Решение уравнений.
1)
График логарифмической функции
Решение уравнений.
1)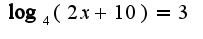 Сначала нужно найти область допустимых значений решений:
Сначала нужно найти область допустимых значений решений: 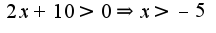 Затем правую часть уравнения представим в виде
Затем правую часть уравнения представим в виде 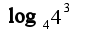 Следовательно, можем приравнять подлогарифмические выражения
Следовательно, можем приравнять подлогарифмические выражения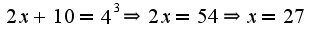 Найденный корень уравнения входит в ОДЗ, можно сделать проверку найденного решения и подставить в уравнение.
Найденный корень уравнения входит в ОДЗ, можно сделать проверку найденного решения и подставить в уравнение.
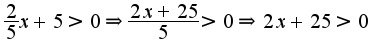
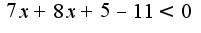
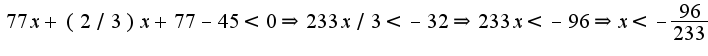
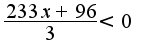 Примеры на дом:
Решить неравенства:
1)
Примеры на дом:
Решить неравенства:
1)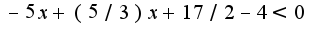 Решение:
Решение:
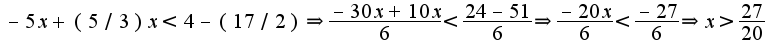 2
2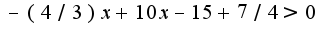 3)
3)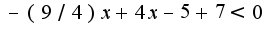 Решить неравенства:
1)
Решить неравенства:
1)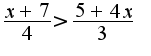 2)
2)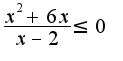
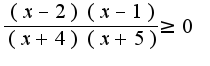 Используем метод интервалов:
1)найдем нули функции:
Используем метод интервалов:
1)найдем нули функции: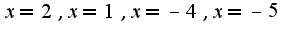 2)нанесем найденные точки на прямую:
3)разобьем действительную прямую на интервалы и определим знак неравенства в каждом интервале eng_1.jpg
2)нанесем найденные точки на прямую:
3)разобьем действительную прямую на интервалы и определим знак неравенства в каждом интервале eng_1.jpg
![$x\in(-\infty,-5)\cup (-4,1]\cup[2,+\infty)$ $x\in(-\infty,-5)\cup (-4,1]\cup[2,+\infty)$](http://teacode.com/service/latex/latex.png?latex=x%5Cin%28-%5Cinfty%2C-5%29%5Ccup+%28-4%2C1%5D%5Ccup%5B2%2C%2B%5Cinfty%29&fontsize=21) 2)
2)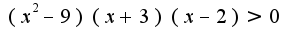
![$x\in (-\infty,-3]\cup[2,3]$ $x\in (-\infty,-3]\cup[2,3]$](http://teacode.com/service/latex/latex.png?latex=x%5Cin+%28-%5Cinfty%2C-3%5D%5Ccup%5B2%2C3%5D&fontsize=21) 3)
3)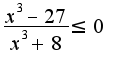 Формулы разность и сумма кубов:
Формулы разность и сумма кубов: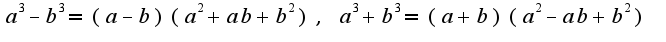 Корни квадратного уравнения:
Корни квадратного уравнения: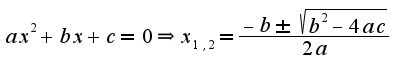 4)
4)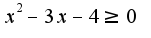 Находим корни соответсвующего уравнения, получим
Находим корни соответсвующего уравнения, получим 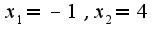 Строим схематично график параболы, т.к. коэффициент при
Строим схематично график параболы, т.к. коэффициент при 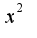 равен 1, то есть положительный, то ветви параболы направлены вверх, поэтому график такой:
Домашняя работа:
решить неравенства.
1)
равен 1, то есть положительный, то ветви параболы направлены вверх, поэтому график такой:
Домашняя работа:
решить неравенства.
1)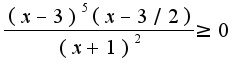 2)
2)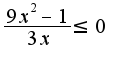
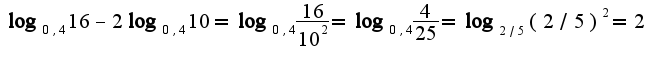
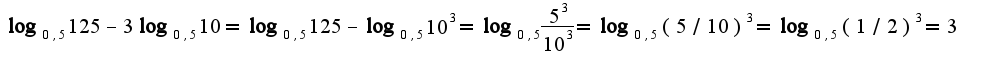 2) Решить уравнение:
2) Решить уравнение:
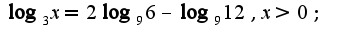
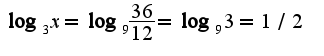
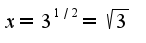 Домашняя работа: параграф 15, №271,275,277, параграф 16, №292,294, параграф 19,№337
Домашняя работа: параграф 15, №271,275,277, параграф 16, №292,294, параграф 19,№337