Поиск
| Автор | Сообщение |
|---|---|
|
Крис
#
7 фев 2017 |
|
|
o_a
#
7 фев 2017 |
|
|
Крис
#
8 фев 2017 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
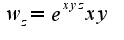 - переменные
- переменные 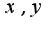 считаются постоянными, аналогично находятся две других частных производных
считаются постоянными, аналогично находятся две других частных производных
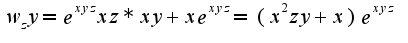
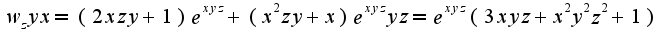 N 3195 решается аналогично, ответ
N 3195 решается аналогично, ответ