Поиск
| Автор | Сообщение |
|---|---|
|
Ирина
#
2 дек 2008 |
|
|
О.А.
#
2 дек 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
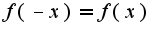 , то коэффициенты ряда Фурье имеют вид:
, то коэффициенты ряда Фурье имеют вид: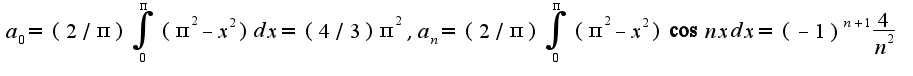 последний интеграл берется по частям, сам ряд имеет вид
последний интеграл берется по частям, сам ряд имеет вид