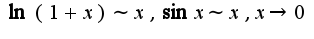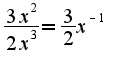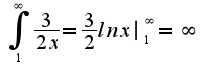Поиск
| Автор | Сообщение |
|---|---|
|
Андрей Викторочич
#
3 июн 2009 |
|
|
О.А.
#
3 июн 2009 |
|
|
Андрей Викторочич
#
4 июн 2009 |
|
|
О.А.
#
4 июн 2009 |
|
|
Андрей Викторочич
#
4 июн 2009 |
|
|
О.А.
#
4 июн 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
![$\int_{1}^{+\infty}\frac{3x^2+\sqrt{(x+1)^3}}{2x^3+\sqrt[3]{x^5}+1}dx$ $\int_{1}^{+\infty}\frac{3x^2+\sqrt{(x+1)^3}}{2x^3+\sqrt[3]{x^5}+1}dx$](http://teacode.com/service/latex/latex.png?latex=%5Cint_%7B1%7D%5E%7B%2B%5Cinfty%7D%5Cfrac%7B3x%5E2%2B%5Csqrt%7B%28x%2B1%29%5E3%7D%7D%7B2x%5E3%2B%5Csqrt%5B3%5D%7Bx%5E5%7D%2B1%7Ddx&fontsize=21) ;
;
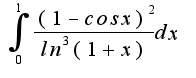 .
Буду очень благодарен!
.
Буду очень благодарен!
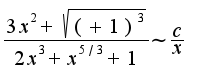 при
при 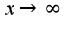 , т.к. интеграл
, т.к. интеграл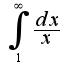 -расходится, то расходится и исходный, аналогично решается второй пример, нужно использовать асимптотику
-расходится, то расходится и исходный, аналогично решается второй пример, нужно использовать асимптотику