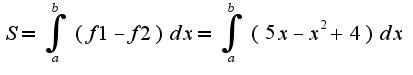| Автор | Сообщение |
|---|---|
|
Ринат
#
17 дек 2009 |
|
|
О.А.
#
17 дек 2009 |
|
|
алиса
#
26 дек 2009 |
|
|
bublik
#
9 мар 2011 |
|
|
o_a
#
9 мар 2011 |
|
|
SKill
#
16 мая 2011 |
|
|
o_a
#
16 мая 2011 |
|
|
SKill
#
18 мая 2011 |
|
|
o_a
#
18 мая 2011 |
|
|
vovantus
#
23 мая 2011 |
|
|
o_a
#
23 мая 2011 |
|
|
vovantus
#
24 мая 2011 |
|
|
saymon15
#
29 мая 2011 |
|
|
Mordecai
#
20 янв 2013 |
|
|
o_a
#
20 янв 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
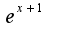 или
или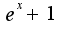 область изменения для переменной
область изменения для переменной  уже известна
уже известна![$x\in[-1,0]$ $x\in[-1,0]$](http://teacode.com/service/latex/latex.png?latex=x%5Cin%5B-1%2C0%5D&fontsize=21) площадь находится по формуле
площадь находится по формуле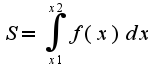
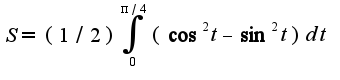
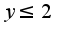 , то
, то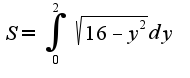 , а если
, а если 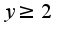 , то
, то 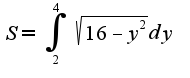 Вычислить интеграл можно, используя подстановку
Вычислить интеграл можно, используя подстановку 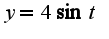
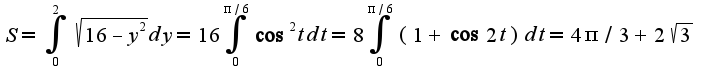
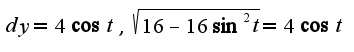 прежде, чем что-то комментировать, надо подумать
прежде, чем что-то комментировать, надо подумать