Поиск
| Автор | Сообщение |
|---|---|
|
Sebastien
#
6 ноя 2008 |
|
|
О.А.
#
6 ноя 2008 |
|
|
Sebastien
#
7 ноя 2008 |
|
|
О.А.
#
7 ноя 2008 |
|
|
Sebastien
#
7 ноя 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
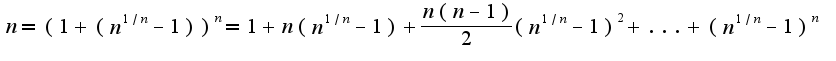 из данного представления получим очевидное неравенство
из данного представления получим очевидное неравенство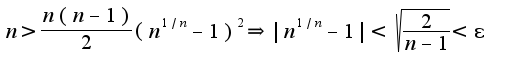 для любого положительного
для любого положительного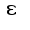 сл-но,
сл-но, 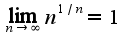
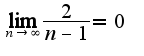 , поэтому
, поэтому 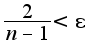 . что следует из определения предела:
. что следует из определения предела: