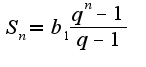Поиск
| Автор | Сообщение |
|---|---|
|
Алёна
#
10 фев 2009 |
|
|
О.А.
#
10 фев 2009 |
|
|
Алёна
#
10 фев 2009 |
|
|
О.А.
#
10 фев 2009 |
|
|
Алёна
#
10 фев 2009 |
|
|
О.А.
#
10 фев 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
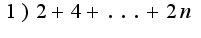
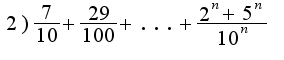
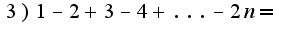
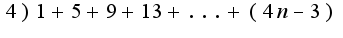 подскажите ещё где можно научиться преобразованию, может есть какая-нибудь хорошая книжка, у меня нет такого
подскажите ещё где можно научиться преобразованию, может есть какая-нибудь хорошая книжка, у меня нет такого
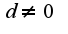 . Иначе говоря, для всех элементов прогрессии, начиная со второго выполнено равенство.
. Иначе говоря, для всех элементов прогрессии, начиная со второго выполнено равенство.
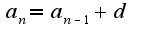 Любой член прогрессии может быть вычислен по формуле:
Любой член прогрессии может быть вычислен по формуле:
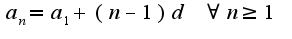 (формула общего члена) Сумма n-слагаемых определяется по формуле:
(формула общего члена) Сумма n-слагаемых определяется по формуле: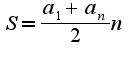 2)-это геометрическая прогрессия. Геометрическая прогрессия — последовательность чисел
2)-это геометрическая прогрессия. Геометрическая прогрессия — последовательность чисел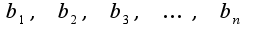 (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число
(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число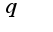 (знаменатель прогрессии), где
(знаменатель прогрессии), где 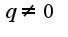 и обычно предполагают ещё что
и обычно предполагают ещё что 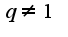
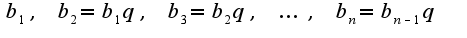 Любой член геометрической прогрессии может быть вычислен по формуле:
Любой член геометрической прогрессии может быть вычислен по формуле:
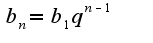 Cумма n-слагаемых определяется по формуле
Cумма n-слагаемых определяется по формуле