Поиск
| Автор | Сообщение |
|---|---|
|
Олег
#
20 мар 2009 |
|
|
О.А.
#
21 мар 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
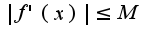 , то по определению предела по Коши получим, что
, то по определению предела по Коши получим, что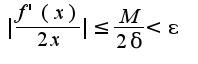 , так как по условию
, так как по условию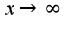 , то
, то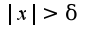 и
и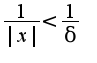 при этом
при этом