Поиск
| Автор | Сообщение |
|---|---|
|
Kira
#
23 фев 2009 |
|
|
О.А.
#
23 фев 2009 |
|
|
Kira
#
23 фев 2009 |
|
|
Kira
#
23 фев 2009 |
|
|
О.А.
#
24 фев 2009 |
|
|
Kira
#
24 фев 2009 |
|
|
Kira
#
24 фев 2009 |
|
|
Irina
#
16 июн 2009 |
|
|
О.А.
#
16 июн 2009 |
|
|
Irina
#
16 июн 2009 |
|
|
Nata
#
8 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
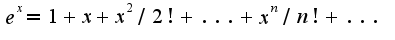 ,т.к. погрешность
,т.к. погрешность 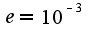 , то из полученных слагаемых надо оставить 4, ответ
, то из полученных слагаемых надо оставить 4, ответ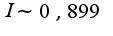
 нужно подставить
нужно подставить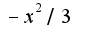 , потом интегрировать
, потом интегрировать