Поиск
| Автор | Сообщение |
|---|---|
|
Егор
#
4 янв 2008 |
|
|
Егор
#
4 янв 2008 |
|
|
О.А.
#
4 янв 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
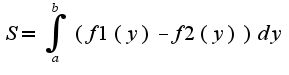 , в данном случае
, в данном случае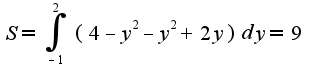 2) нужно параметризовать кривую,т.е.
2) нужно параметризовать кривую,т.е. 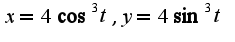 ,длина дуги кривой, заданной параметрически,находится по формуле
,длина дуги кривой, заданной параметрически,находится по формуле