Поиск
| Автор | Сообщение |
|---|---|
|
Noname
#
9 дек 2016 |
|
|
o_a
#
9 дек 2016 |
|
|
Noname
#
12 дек 2016 |
|
|
o_a
#
12 дек 2016 |
|
|
Noname
#
12 дек 2016 |
|
|
o_a
#
12 дек 2016 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
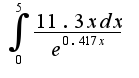 ?
?
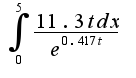 . Ответ задачи известен, но нужно решение. Спасибо.
. Ответ задачи известен, но нужно решение. Спасибо.
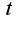 в формуле? Если производительность труда имеет вид
в формуле? Если производительность труда имеет вид 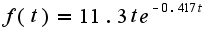 , то объем выпуска за 5 часов определяется по формуле
, то объем выпуска за 5 часов определяется по формуле 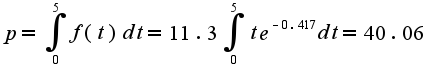 интегрирование производится по частям (метод есть в любой литературе по математическому анализу)
интегрирование производится по частям (метод есть в любой литературе по математическому анализу)
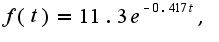 то соответственно
то соответственно 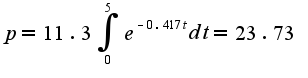 интеграл берется по таблице основных интегралов
интеграл берется по таблице основных интегралов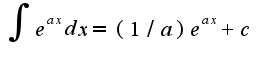 и применяется формула Ньютона-Лейбница для определенного интеграла
и применяется формула Ньютона-Лейбница для определенного интеграла