Поиск
| Автор | Сообщение |
|---|---|
|
distvamp
#
27 ноя 2016 |
|
|
o_a
#
27 ноя 2016 |
|
|
distvamp
#
27 ноя 2016 |
|
|
Tina
#
3 мар 2017 |
|
|
o_a
#
3 мар 2017 |
|
|
Tina
#
3 мар 2017 |
|
|
o_a
#
3 мар 2017 |
|
|
Tina
#
4 мар 2017 |
|
|
Tina
#
4 мар 2017 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
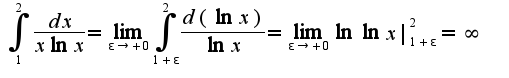 Сл-но, данный интеграл расходится
Сл-но, данный интеграл расходится
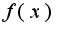 непрерывна и имеет ограниченную первообразную;
2) функция
непрерывна и имеет ограниченную первообразную;
2) функция 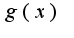 непрерывно дифференцируема и убывает, стремясь к нулю при
непрерывно дифференцируема и убывает, стремясь к нулю при 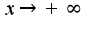 , т. е.
, т. е.
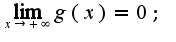 то интеграл
то интеграл 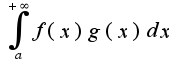 -cх-ся
Достаточно выбрать
-cх-ся
Достаточно выбрать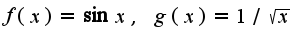 2) интеграл расходится по определению несобстенного интеграла второго рода(см. теорию в любом учебнике по математическому анализу)
2) интеграл расходится по определению несобстенного интеграла второго рода(см. теорию в любом учебнике по математическому анализу)
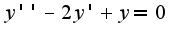 , составляя алгебраическое
, составляя алгебраическое 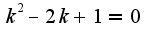 Решая, имеем
Решая, имеем 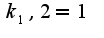 Поэтому общее решение однородного уравнения имеет вид
Поэтому общее решение однородного уравнения имеет вид 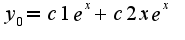 Затем ищут частное решение неоднородного уравнения, используя либо метод вариации произвольных констант, либо исходя из вида правой части (методы описаны в любом задачнике по д.у.)
Затем ищут частное решение неоднородного уравнения, используя либо метод вариации произвольных констант, либо исходя из вида правой части (методы описаны в любом задачнике по д.у.)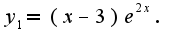 Таким образом, общее решение неоднородного уравнения имеет вид:
Таким образом, общее решение неоднородного уравнения имеет вид: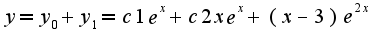 Осталось найти произвольные константы
Осталось найти произвольные константы 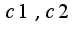 , используя данные задачи
, используя данные задачи 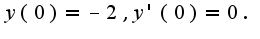 Составляя равенства, исходя из полученного вида решения, получим, что
Составляя равенства, исходя из полученного вида решения, получим, что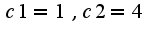 . Сл-но, частное решение неоднородного уравнения имеет вид
. Сл-но, частное решение неоднородного уравнения имеет вид