Поиск
| Автор | Сообщение |
|---|---|
|
cтудeнтка
#
6 июн 2006 |
|
|
cтудeнтка
#
6 июн 2006 |
|
|
О.А.
#
6 июн 2006 |
|
|
cтудeнтка
#
7 июн 2006 |
|
|
ната
#
16 июн 2006 |
|
|
ната
#
16 июн 2006 |
|
|
ната
#
16 июн 2006 |
|
|
ната
#
16 июн 2006 |
|
|
ната
#
16 июн 2006 |
|
|
Вика
#
17 июн 2006 |
|
|
Вика
#
17 июн 2006 |
|
|
О.А.
#
17 июн 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
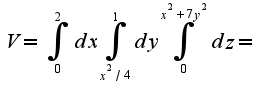
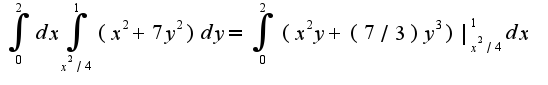
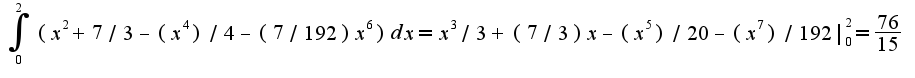
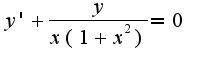 Данное уравнение -с разделяющимися переменными:
Данное уравнение -с разделяющимися переменными: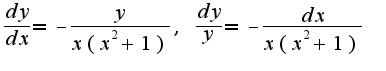
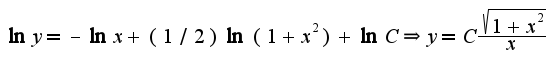 2)Затем используют метод вариации произвольной константы C,т.е. подставляют в уравнение найденное решение, считая, что C(x)зависит от x.Легко найти
2)Затем используют метод вариации произвольной константы C,т.е. подставляют в уравнение найденное решение, считая, что C(x)зависит от x.Легко найти