Поиск
| Автор | Сообщение |
|---|---|
|
Костя
#
16 дек 2006 |
|
|
О.А.
#
16 дек 2006 |
|
|
Костя
#
16 дек 2006 |
|
|
О.А.
#
16 дек 2006 |
|
|
Костя
#
17 дек 2006 |
|
|
О.А.
#
17 дек 2006 |
|
|
Дима
#
19 ноя 2007 |
|
|
Дима
#
19 ноя 2007 |
|
|
Анатолий
#
19 ноя 2007 |
|
|
максим
#
11 янв 2008 |
|
|
О.А.
#
11 янв 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
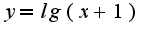
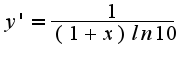
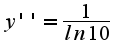
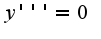 Остановиться на производной второго или третьего порядка?:)
Остановиться на производной второго или третьего порядка?:)
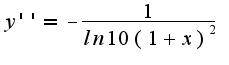
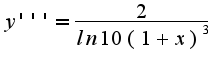 Но так можно вечно находить производные...и четвёртого...и сотого порядков...разве так должно быть?
Но так можно вечно находить производные...и четвёртого...и сотого порядков...разве так должно быть?
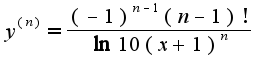
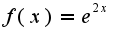 , то сами смотрите:
, то сами смотрите:
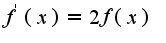
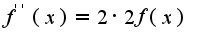 ...
...
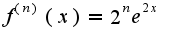
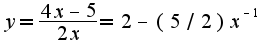 тогда
тогда