Поиск
| Автор | Сообщение |
|---|---|
|
Александр
#
25 дек 2006 |
|
|
О.А.
#
25 дек 2006 |
|
|
Александр
#
25 дек 2006 |
|
|
О.А.
#
25 дек 2006 |
|
|
Оля
#
28 дек 2006 |
|
|
О.А.
#
28 дек 2006 |
|
|
Оля
#
28 дек 2006 |
|
|
Оля
#
28 дек 2006 |
|
|
Оля
#
28 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
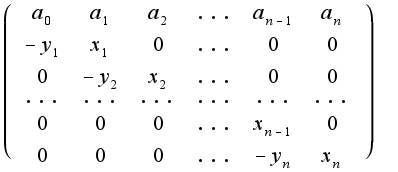
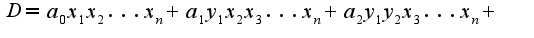
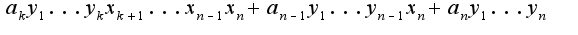
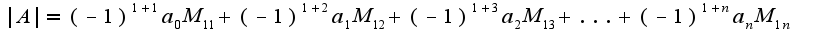 Далее я считала каждые слагаемые и соответствующие миноры, с первыми двумя слагаемыми проблем не возникло, определители M_{11} M_{12} получились равны произведению диагональных элементов, а вот с третьим не знаю..
1)
Далее я считала каждые слагаемые и соответствующие миноры, с первыми двумя слагаемыми проблем не возникло, определители M_{11} M_{12} получились равны произведению диагональных элементов, а вот с третьим не знаю..
1) 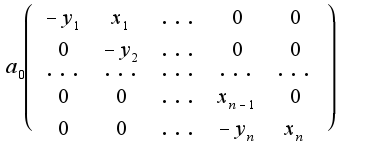 Здесь уже нельзя будет определитель посчитать как произведение диагональных элементов, поскольку мешаются и
Здесь уже нельзя будет определитель посчитать как произведение диагональных элементов, поскольку мешаются и 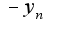 и
и 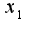 , лежащие по разные стороны от главной диагонали. Как быть в этом случае, не могли бы вы посчитать этот минор, а также миноры со множителями
, лежащие по разные стороны от главной диагонали. Как быть в этом случае, не могли бы вы посчитать этот минор, а также миноры со множителями 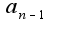 и
и 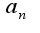 , у меня не получается…заранее спасибо, Ольга Александровна, с наступающим!
, у меня не получается…заранее спасибо, Ольга Александровна, с наступающим!
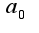 и
и