Поиск
| Автор | Сообщение |
|---|---|
|
Оля
#
6 апр 2007 |
|
|
О.А.
#
6 апр 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
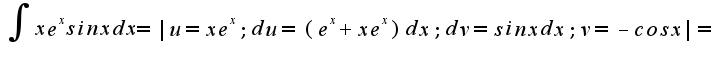
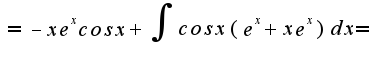
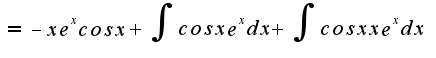
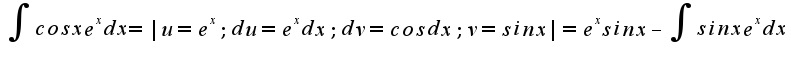
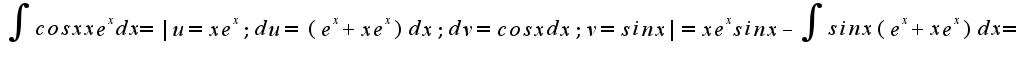
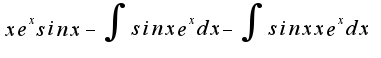
![$2\int{xe^xsinxdx}=-xe^xcosx+e^xsinx- 2[\int{sinx e^xdx}] +xe^xsinx$ $2\int{xe^xsinxdx}=-xe^xcosx+e^xsinx- 2[\int{sinx e^xdx}] +xe^xsinx$](http://teacode.com/service/latex/latex.png?latex=2%5Cint%7Bxe%5Exsinxdx%7D%3D-xe%5Excosx%2Be%5Exsinx-+2%5B%5Cint%7Bsinx+e%5Exdx%7D%5D+%2Bxe%5Exsinx&fontsize=21)
![$[\int{sinx e^xdx}]=|u=e^x; du=e^xdx; dv=sinx; v=-cosx|=-e^xcosx+\int{e^xcosxdx}=$ $[\int{sinx e^xdx}]=|u=e^x; du=e^xdx; dv=sinx; v=-cosx|=-e^xcosx+\int{e^xcosxdx}=$](http://teacode.com/service/latex/latex.png?latex=%5B%5Cint%7Bsinx+e%5Exdx%7D%5D%3D%7Cu%3De%5Ex%3B+du%3De%5Exdx%3B+dv%3Dsinx%3B+v%3D-cosx%7C%3D-e%5Excosx%2B%5Cint%7Be%5Excosxdx%7D%3D&fontsize=21)
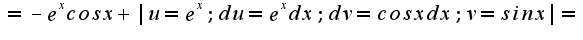
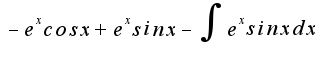
![$[\int{sinx e^xdx}]=(-e^xcosx+e^xsinx)/2$ $[\int{sinx e^xdx}]=(-e^xcosx+e^xsinx)/2$](http://teacode.com/service/latex/latex.png?latex=%5B%5Cint%7Bsinx+e%5Exdx%7D%5D%3D%28-e%5Excosx%2Be%5Exsinx%29%2F2&fontsize=21)
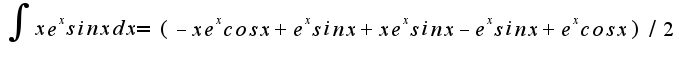 =
=