Поиск
| Автор | Сообщение |
|---|---|
|
Ольга
#
4 ноя 2007 |
|
|
Анатолий
#
4 ноя 2007 |
|
|
Анатолий
#
4 ноя 2007 |
|
|
Ольга
#
4 ноя 2007 |
|
|
Ольга
#
4 ноя 2007 |
|
|
Анатолий
#
4 ноя 2007 |
|
|
Ольга
#
4 ноя 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
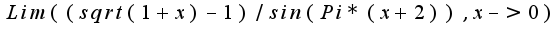 . Пробовала решать этот предел с применением эквивалентности и домножая на сопряженное , и не могу никак добиться правильного ответа, получается ноль, а правильный ответ (1/(2*Pi)). Подскажите в чем ошибка, или как открыть неопределенность.
2. А с этим пределом даже мыслей нет, просто загнал в тупик
. Пробовала решать этот предел с применением эквивалентности и домножая на сопряженное , и не могу никак добиться правильного ответа, получается ноль, а правильный ответ (1/(2*Pi)). Подскажите в чем ошибка, или как открыть неопределенность.
2. А с этим пределом даже мыслей нет, просто загнал в тупик
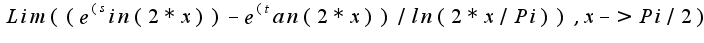 Видела просьбу решить похожий предел, но ответа так и не нашла.
Если есть идеи, поделитесь, пожалуйста.
За ранее спасибо.
С ув., Ольга.
Видела просьбу решить похожий предел, но ответа так и не нашла.
Если есть идеи, поделитесь, пожалуйста.
За ранее спасибо.
С ув., Ольга.
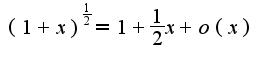
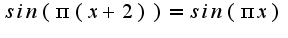 В следствие
В следствие 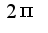 - перbодичности синуса.
- перbодичности синуса.
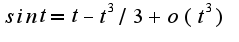
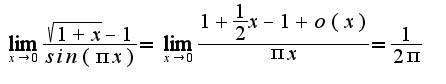
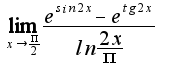
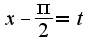 и перепишем предел следующим образом:
и перепишем предел следующим образом:
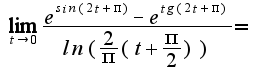
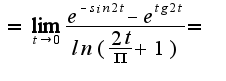
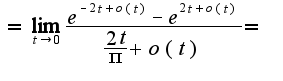
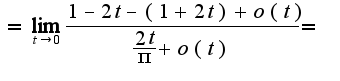
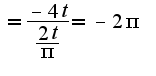 Использовалось:
Использовалось:
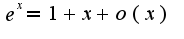
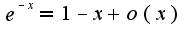
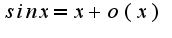
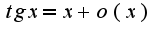
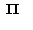 -периодична
-периодична