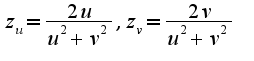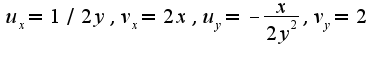Поиск
| Автор | Сообщение |
|---|---|
|
Алексей
#
5 мар 2011 |
|
|
o_a
#
5 мар 2011 |
|
|
Алексей
#
5 мар 2011 |
|
|
ААФ
#
7 мая 2011 |
|
|
o_a
#
7 мая 2011 |
|
|
ААФ
#
7 мая 2011 |
|
|
anuttka
#
23 мая 2011 |
|
|
vovantus
#
23 мая 2011 |
|
|
anuttka
#
24 мая 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
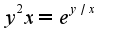
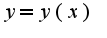 , затем разрешают полученное уравнение относительно
, затем разрешают полученное уравнение относительно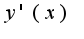 Дифференцируя данное уравнение, получим:
Дифференцируя данное уравнение, получим: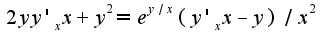 Решаем данное уравнение относительно
Решаем данное уравнение относительно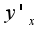 :
: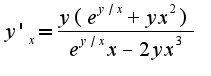
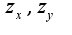 , то нужно находить производные по формулам:
, то нужно находить производные по формулам: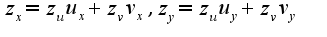 В данные формулы подставить найденные частные производные:
В данные формулы подставить найденные частные производные: