Поиск
| Автор | Сообщение |
|---|---|
|
Нефедьев И.В.
#
6 дек 2005 |
|
|
О.А.
#
6 дек 2005 |
|
|
Нефедьев
#
16 дек 2005 |
|
|
О.А.
#
16 дек 2005 |
|
|
Нефедьев
#
23 дек 2005 |
|
|
О.А.
#
23 дек 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
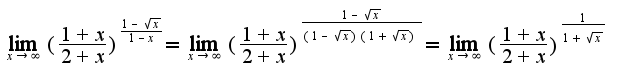 Переходим к пределу в основании и в показателе при
Переходим к пределу в основании и в показателе при 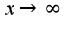 Получим, что
Получим, что 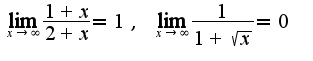 Поэтому
Поэтому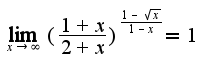 Чтобы доказать, что
Чтобы доказать, что 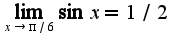 надо использовать определение предела на языке
надо использовать определение предела на языке 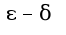 :
: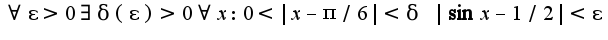 Затем преобразовать разность синусов в произведение,
Затем преобразовать разность синусов в произведение, 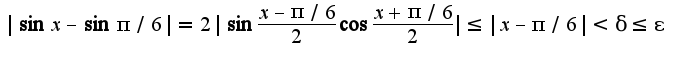 То есть,
То есть, 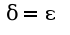
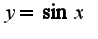 Т.к. предел равен 1/2, то
Т.к. предел равен 1/2, то 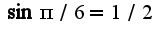 , ну и затем конкретное применение определения, записывается разность синусов и учитывается неравенства:
, ну и затем конкретное применение определения, записывается разность синусов и учитывается неравенства: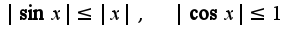 Т.к
Т.к 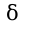 , при котором выполнится необходимое неравенство, что означает, что
, при котором выполнится необходимое неравенство, что означает, что