Поиск
| Автор | Сообщение |
|---|---|
|
alexandra555
#
30 окт 2011 |
|
|
o_a
#
30 окт 2011 |
|
|
alexandra555
#
8 ноя 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
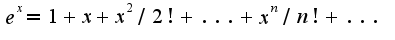 , 2) представить данную дробь как сумму бесконечно убывающей прогрессии со знаменателем
, 2) представить данную дробь как сумму бесконечно убывающей прогрессии со знаменателем 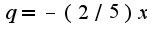 Для нахождения области сходимости можно использовать формулу радиуса сходимости
Для нахождения области сходимости можно использовать формулу радиуса сходимости 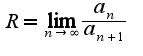 , где
, где 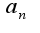 -коэффициент ряда
-коэффициент ряда