Поиск
| Автор | Сообщение |
|---|---|
|
Катя
#
6 дек 2009 |
|
|
О.А.
#
6 дек 2009 |
|
|
Юлия
#
6 дек 2009 |
|
|
Юлия
#
6 дек 2009 |
|
|
Катя
#
6 дек 2009 |
|
|
О.А.
#
6 дек 2009 |
|
|
Катя
#
6 дек 2009 |
|
|
О.А.
#
7 дек 2009 |
|
|
Катя
#
7 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
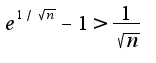 ряд
ряд 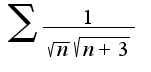 расходится, поэтому расходится и исходный ряд
2) если предел вида
расходится, поэтому расходится и исходный ряд
2) если предел вида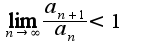 то ряд сходится
то ряд сходится
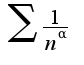 сходится при
сходится при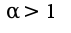 и расходится при
и расходится при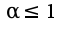 это известный факт, загляните в учебник по высшей математике, данный ряд называется обобщенный гармонический
2) что касается нахождения предела, то рекомендую составить отношение и найти предел, за вас решать я не буду, могу проверить нахождение предела
это известный факт, загляните в учебник по высшей математике, данный ряд называется обобщенный гармонический
2) что касается нахождения предела, то рекомендую составить отношение и найти предел, за вас решать я не буду, могу проверить нахождение предела
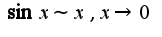 ,следовательно,
,следовательно,