Форумы > Консультация по матанализу > Дифференциальные уравнения

Страницы: 1 2 3

Поиск
Автор Сообщение
Настена #
18 июн 2008
вот решение в нормальном виде. гляньте пожалуйста нет ли ошибок http://ipicture.ru/uploads/080618/9Rglv4zTnS.jpg
О.А. #
18 июн 2008
производная от частного решения найдена неверно
Настена #
18 июн 2008
А какие там должны быть производные? подскажите, пожалуйста!!
О.А. #
18 июн 2008
$y'=e^{-3x}((-3A+B)\cos x-(3B+A)\sin x)$
Настена #
18 июн 2008
А вторая?
аноним #
19 июн 2008
Настёна, попробуй сама, что ты совсем расслабилась
Настена #
19 июн 2008
Да у меня только с производными траблы, дальше я знаю чего делать... Из-за неправильно найденных выше указанных у меня и пошли все ошибки :(
О.А. #
19 июн 2008
тем более надо научиться брать производные, то что за вас кто-то решит, не поможет
аноним #
19 июн 2008
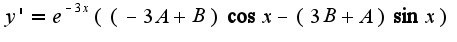
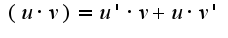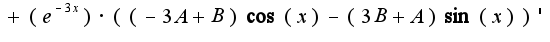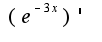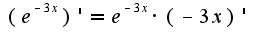у тебя произведение, находишь производную по правилу $(u \cdot v)=u' \cdot v + u \cdot v'$ у тебя $y'=(e^{-3x})' \cdot ((-3A+B)\cos(x)-(3B+A)\sin(x))+$ $+(e^{-3x}) \cdot ((-3A+B)\cos(x)-(3B+A)\sin(x))'$ у тебя проблема вычислить $(e^{-3x})'$ ? она вычисляется как производная от сложной функции: $(e^{-3x})'= e^{-3x} \cdot (-3x)'$ довычисляй, и пиши что получается, сравню со своим ответом
Настена #
19 июн 2008
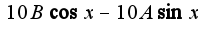$10B\cos x-10A\sin x$ так?
аноним #
19 июн 2008
напиши как вычисляла (если время позволяет), заодно укажу где ошиблась, по себе знаю - помогает, глядишь - разберёшься. давай, понабирай, я подожду (честно)
Настена #
19 июн 2008
А сейчас пересчитала и получилось (8A-6B)cosx + (6A+8B)sinx
аноним #
19 июн 2008
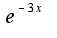Всё правильно, молодец, только вы потеряли $e^{-3x}$ будет так: 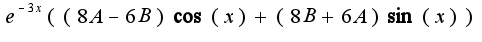$e^{-3x}((8A-6B)\cos(x)+(8B+6A)\sin(x))$ ну всё, обещание сдержала, пойду-ка я спать (у меня уже время 0.32)
Настена #
19 июн 2008
про е я помню :) спасибо за помощь. приятных снов
аноним #
19 июн 2008
удачи вам дорешать диф.ур.

Страницы: 1 2 3

Форумы > Консультация по матанализу > Дифференциальные уравнения
Чтобы написать сообщение, необходимо войти или зарегистрироваться

© teacode.com, 2004-2016