Поиск
| Автор | Сообщение |
|---|---|
|
Наташа
#
22 сен 2013 |
|
|
o.a.
#
22 сен 2013 |
|
|
Наташа
#
25 сен 2013 |
|
|
Наталья Хушеева
#
17 окт 2013 |
|
|
o.a.
#
17 окт 2013 |
|
|
o.a.
#
17 окт 2013 |
|
|
Наталья Хушеева
#
19 окт 2013 |
|
|
Наталья Хушеева
#
20 окт 2013 |
|
|
o.a.
#
20 окт 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
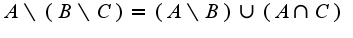 один из вариантов решения
один из вариантов решения 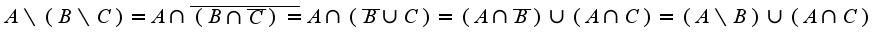
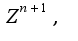 получим 6иекцию между множеством всех многочленов An степени не выше n и декартовым произведением
получим 6иекцию между множеством всех многочленов An степени не выше n и декартовым произведением 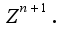 Отсюда в силу счетности множества
Отсюда в силу счетности множества 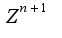 следует счётность множества An. Так как множество всех многочленов с целыми коэффициентами представляется, очевидно,в виде
следует счётность множества An. Так как множество всех многочленов с целыми коэффициентами представляется, очевидно,в виде 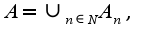 то по свойствам счетных множеств множество A счётно.
то по свойствам счетных множеств множество A счётно.