Поиск
| Автор | Сообщение |
|---|---|
|
Студент
#
17 мар 2008 |
|
|
О.А.
#
17 мар 2008 |
|
|
Студент
#
18 мар 2008 |
|
|
asdf
#
26 мар 2008 |
|
|
О.А.
#
26 мар 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
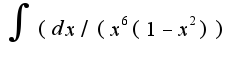 Подскажите, пожалуйста, какую лучше выполнить здесь замену?
Подскажите, пожалуйста, какую лучше выполнить здесь замену?
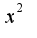 ,т.е.
,т.е.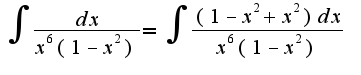 затем почленно поделить,получим
затем почленно поделить,получим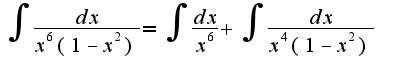 затем дважды проделать вышеуказанное преобразование, получим
затем дважды проделать вышеуказанное преобразование, получим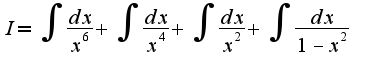
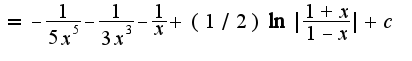
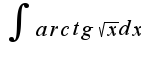
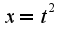 , затем интегрируйте по частям
, затем интегрируйте по частям