Ряды

Автор	Сообщение
Альбина # 11 дек 2008	Помогите пожалуста с рядами Исследовать сходимость ряда: Сумма от бесконечности до К=1 (2К)!/(К!)^2 Найти области сходимости рядов: Сумма от бесконечности до К=1 Х^К/(2К)! Разложить в ряд Маклорена 1/Х+2 Спасибо
О.А. # 11 дек 2008	рекомендую посмотреть сборник задач по математическому анализу под редакцией Кудрявцева Л.Д., подобные примеры там решены
Фанис # 11 дек 2008	тогда вопрос такой: Можно ли разложить(2n)! на 2!*n!
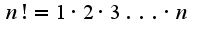О.А. # 12 дек 2008	ну, конечно, нет $n!=1\cdot2\cdot3...\cdot n$ в данном примере примените признак Даламбера: если предел 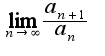$\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_{n}}$ меньше 1, то ряд сходится, если >1, то расходится
Ваш ответ:	Чтобы написать сообщение, необходимо войти или зарегистрироваться

Чтобы написать сообщение, необходимо войти или зарегистрироваться

Teacode.com: Ряды