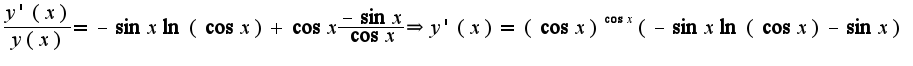Поиск
| Автор | Сообщение |
|---|---|
|
Елена
#
22 янв 2009 |
|
|
О.А.
#
22 янв 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
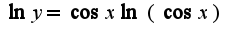 , затем находят производную от обеих частей
, затем находят производную от обеих частей