Поиск
| Автор | Сообщение |
|---|---|
|
777
#
20 ноя 2005 |
|
|
О.А.
#
20 ноя 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
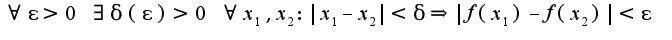 Для данной функции:
Для данной функции: 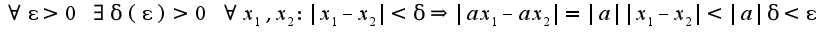 Т.е.
Т.е. 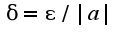 . Сл-но, выполняется определение равномерно непрерывной функции.
. Сл-но, выполняется определение равномерно непрерывной функции.