| Автор | Сообщение |
|---|---|
|
Катя
#
19 апр 2006 |
|
|
О.А.
#
19 апр 2006 |
|
|
SmArt
#
19 апр 2006 |
|
|
О.А.
#
20 апр 2006 |
|
|
Катя
#
20 апр 2006 |
|
|
О.А.
#
20 апр 2006 |
|
|
Катя
#
21 апр 2006 |
|
|
SmArt
#
21 апр 2006 |
|
|
SmArt
#
21 апр 2006 |
|
|
О.А.
#
21 апр 2006 |
|
|
Любопытный человек
#
22 апр 2006 |
|
|
О.А.
#
22 апр 2006 |
|
|
Ленок
#
20 фев 2008 |
|
|
Сергей
#
20 фев 2008 |
|
|
Елена
#
21 фев 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
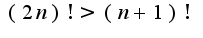 , то
, то 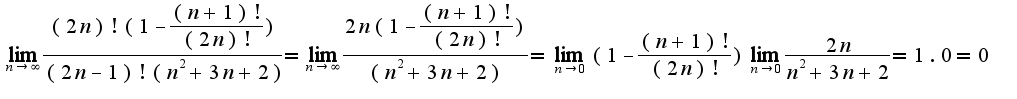
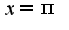 , то надо просто подставить в нее значение
, то надо просто подставить в нее значение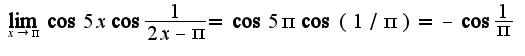
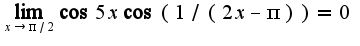 Так как есть свойство бесконечно малых функций:произведение бесконечно малой функции на ограниченную это есть бесконечно малая функция. Учитывая, что
Так как есть свойство бесконечно малых функций:произведение бесконечно малой функции на ограниченную это есть бесконечно малая функция. Учитывая, что 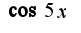 при
при 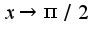 -бесконечно малая функция, а функция
-бесконечно малая функция, а функция 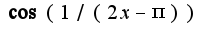 -ограниченная, получим, что предел равен нулю.
-ограниченная, получим, что предел равен нулю.
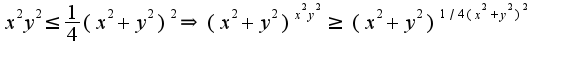 при
при 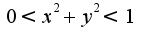 Но,
Но, 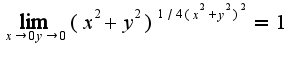 Поэтому
Поэтому