Поиск
| Автор | Сообщение |
|---|---|
|
О.А.
#
29 ноя 2004 |
|
|
Миша
#
2 дек 2004 |
|
|
О.А.
#
2 дек 2004 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
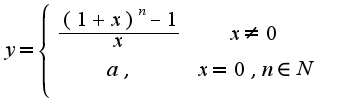 Находим предел функции
Находим предел функции 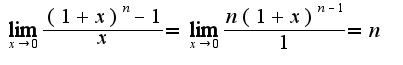 . Поэтому
. Поэтому 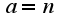 6)
6) 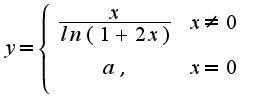 Находим предел
Находим предел 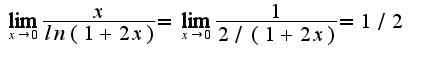 . Следовательно,
. Следовательно, 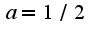 7)
7)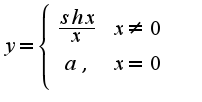 Аналогично,
Аналогично, 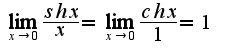 Поэтому
Поэтому 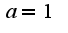
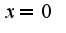 ) в функцию, при этом надо помнить, что постоянное число выносится за знак предела и предел постоянной равен этой постоянной, т.е.
) в функцию, при этом надо помнить, что постоянное число выносится за знак предела и предел постоянной равен этой постоянной, т.е.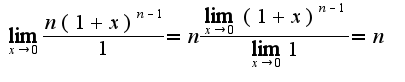 . После вычисления предела функции надо вспомнить определение непрерывной функции, а именно:
. После вычисления предела функции надо вспомнить определение непрерывной функции, а именно: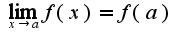 . По условию задачи значение в точке 0 равно a, следовательно,
. По условию задачи значение в точке 0 равно a, следовательно,