Поиск
| Автор | Сообщение |
|---|---|
|
Евгений
#
14 июн 2006 |
|
|
О.А.
#
14 июн 2006 |
|
|
Евгений
#
14 июн 2006 |
|
|
Евгений
#
16 июн 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
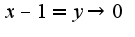 Тогда
Тогда 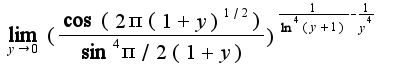 Затем использовать известные разложения для
Затем использовать известные разложения для 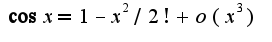 и
и 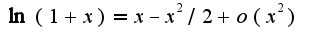 Отсюда получим, что
Отсюда получим, что 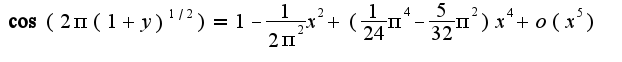
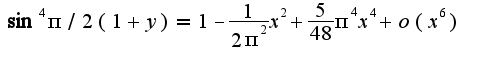 ,
, 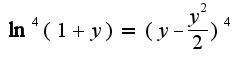 После подстановки в предел предварительно используя соотношение:
После подстановки в предел предварительно используя соотношение: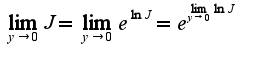 Получим, что предел данной функции равен
Получим, что предел данной функции равен