Поиск
lafum
#
7 окт 2014
|
Ольга Александровна,доброго времени суток!
У меня возник вопрос при решении домашнего задания.
Задание звучит так:
Доказать сходимость последовательности и найти ее предел если:
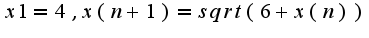 (задание 8.247 (1) страница 226, Л.Д.Кудрявцев)
Вопрос в том, зачем нам дано x1 и почему дано x(n+1), а не x(n)?
|
o_a
#
7 окт 2014
|
Здравствуйте!
Такое задание последовательности называется рекуррентным. Важным способом задания последовательности является так называемый рекуррентный способ, при котором задается выражение, связывающее n-ый член последовательности с одним или несколькими предыдущими. Слово рекуррентный происходит от латинского слова рекурсия, что означает возврат. Вычисляя новый, очередной член последовательности, мы как бы возвращаемся назад, к уже вычисленным, предыдущим членам.
Задан первый элемент последовательности 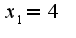 , последующий элемент вычисляется по заданной формуле 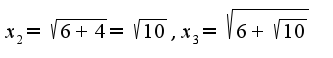 и т.д. Для исследования данной последовательности на сходимость надо применить теорему Вейерштрасса о существовании предела у монотонной последовательности, т.е. установить характер монотонности и ограниченность.
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
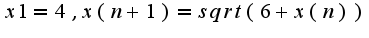 (задание 8.247 (1) страница 226, Л.Д.Кудрявцев)
Вопрос в том, зачем нам дано x1 и почему дано x(n+1), а не x(n)?
(задание 8.247 (1) страница 226, Л.Д.Кудрявцев)
Вопрос в том, зачем нам дано x1 и почему дано x(n+1), а не x(n)?
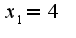 , последующий элемент вычисляется по заданной формуле
, последующий элемент вычисляется по заданной формуле 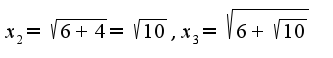 и т.д. Для исследования данной последовательности на сходимость надо применить теорему Вейерштрасса о существовании предела у монотонной последовательности, т.е. установить характер монотонности и ограниченность.
и т.д. Для исследования данной последовательности на сходимость надо применить теорему Вейерштрасса о существовании предела у монотонной последовательности, т.е. установить характер монотонности и ограниченность.