Поиск
| Автор | Сообщение |
|---|---|
|
Миша.
#
24 дек 2006 |
|
|
О.А.
#
19 дек 2006 |
|
|
Миша.
#
24 янв 2007 |
|
|
Миша.
#
24 дек 2006 |
|
|
О.А.
#
20 дек 2006 |
|
|
Миша.
#
22 дек 2006 |
|
|
Миша.
#
22 дек 2006 |
|
|
О.А.
#
22 дек 2006 |
|
|
Миша.
#
19 янв 2007 |
|
|
О.А.
#
23 дек 2006 |
|
|
Миша.
#
23 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
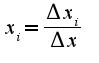 ,где
,где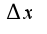 -детерминант самой матрицы, а
-детерминант самой матрицы, а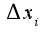 -детерминанты полученные заменой соответствующих столбцов на столбец свободных членов. Если
-детерминанты полученные заменой соответствующих столбцов на столбец свободных членов. Если 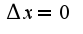 и все
и все 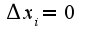 , то решений бесконечное множество, что следует из вышеуказанного равенства.
, то решений бесконечное множество, что следует из вышеуказанного равенства.