Поиск
| Автор | Сообщение |
|---|---|
|
zipo666
#
4 дек 2011 |
|
|
o_a
#
4 дек 2011 |
|
|
абвгдейка
#
11 дек 2011 абвгдейка
11 дек 2011
|
|
|
o_a
#
11 дек 2011 |
|
|
абвгдейка
#
11 дек 2011 |
|
|
o_a
#
11 дек 2011 |
|
|
o_a
#
11 дек 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
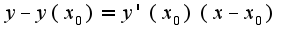 (решаю,получаются очень большие дроби,которые впоследствии не сокращаются)
(решаю,получаются очень большие дроби,которые впоследствии не сокращаются)
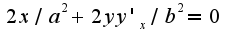
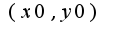 и на этом можно ограничиться
и на этом можно ограничиться