Поиск
| Автор | Сообщение |
|---|---|
|
loz09
#
13 мая 2013 |
|
|
o.a.
#
13 мая 2013 |
|
|
loz09
#
13 мая 2013 |
|
|
o.a.
#
13 мая 2013 |
|
|
loz09
#
13 мая 2013 |
|
|
loz09
#
14 мая 2013 |
|
|
loz09
#
16 мая 2013 |
|
|
Анюша
#
30 июн 2013 |
|
|
o.a.
#
30 июн 2013 |
|
|
alexxx
#
14 окт 2013 |
|
|
o.a.
#
15 окт 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
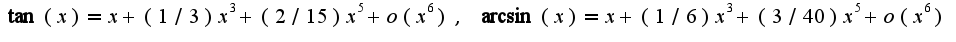 Ответ:-60
Ответ:-60
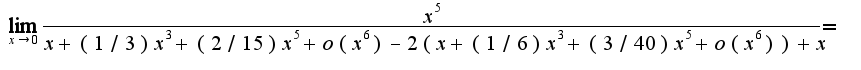
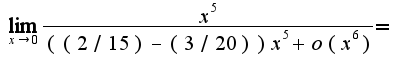
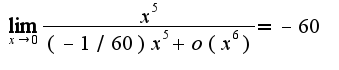
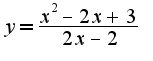 , то надо использовать формулу производная от дроби
, то надо использовать формулу производная от дроби 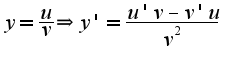 Следуя формуле, получим
Следуя формуле, получим 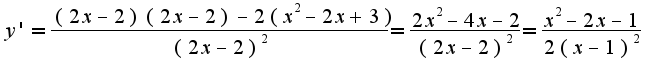
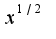 ), затем использовать асимптотическое равенство
), затем использовать асимптотическое равенство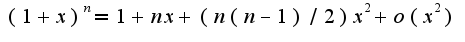 4)сделать замену
4)сделать замену 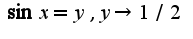 5)привести к пределу
5)привести к пределу