Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
Заочник
#
10 мая 2008 |
|
|
О.А.
#
10 мая 2008 |
|
|
Заочник
#
10 мая 2008 |
|
|
Заочник
#
11 мая 2008 |
|
|
Заочник
#
11 мая 2008 |
|
|
Заочник
#
11 мая 2008 |
|
|
Заочник
#
12 мая 2008 |
|
|
Артём
#
18 мая 2008 |
|
|
О.А.
#
18 мая 2008 |
|
|
Артём
#
18 мая 2008 |
|
|
О.А.
#
19 мая 2008 |
|
|
Артём
#
19 мая 2008 |
|
|
О.А.
#
19 мая 2008 |
|
|
Артём
#
21 мая 2008 |
|
|
Артём
#
21 мая 2008 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
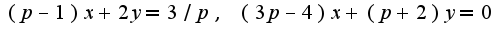 Решая данную систему относительно переменных
Решая данную систему относительно переменных 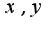 , получим
, получим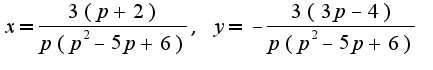 Перейдем в пространство оригиналов, предварительно разлагая на сумму дробей:
Перейдем в пространство оригиналов, предварительно разлагая на сумму дробей: