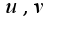Поиск
| Автор | Сообщение |
|---|---|
|
Ольга
#
25 мая 2009 |
|
|
О.А.
#
25 мая 2009 |
|
|
Ольга
#
25 мая 2009 |
|
|
О.А.
#
25 мая 2009 |
|
|
Ольга
#
25 мая 2009 |
|
|
О.А.
#
25 мая 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
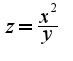 где
где 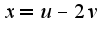 ,
, 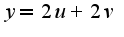 У меня в конце получается чушь.
Можно ли сначала сократить так:
У меня в конце получается чушь.
Можно ли сначала сократить так: 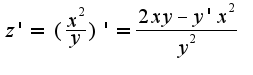 , а уже потом подставлять вместо
, а уже потом подставлять вместо  и
и 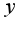 выражения, или их сразу подставлять?
выражения, или их сразу подставлять?
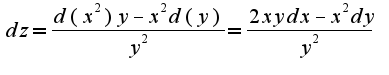 затем в найденный дифференциал нужно подставить
затем в найденный дифференциал нужно подставить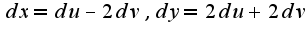 все выражение после преобразования будет зависеть от пременных
все выражение после преобразования будет зависеть от пременных