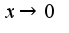Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
О.А.
#
25 ноя 2005 |
|
|
???
#
25 ноя 2005 |
|
|
Кто_я?
#
5 дек 2005 |
|
|
О.А.
#
5 дек 2005 |
|
|
Попов Дмитрий
#
5 дек 2005 |
|
|
О.А.
#
5 дек 2005 |
|
|
У меня вопрос
#
9 дек 2005 |
|
|
Зачем_мне_ник
#
9 дек 2005 |
|
|
О.А.
#
9 дек 2005 |
|
|
О.А.
#
9 дек 2005 |
|
|
.
#
11 дек 2005 |
|
|
О.А.
#
11 дек 2005 |
|
|
Зачем_мне_ник
#
18 дек 2005 |
|
|
О.А.
#
18 дек 2005 |
|
|
я
#
19 дек 2005 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
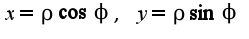 . Тогда
. Тогда 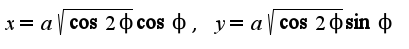 Затем использовать формулу дифференцирования параметрически заданной функции:
Затем использовать формулу дифференцирования параметрически заданной функции: 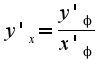 В задаче нужно вычислить правостороннюю производную в тоске
В задаче нужно вычислить правостороннюю производную в тоске 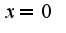 , чтобы найти точки, где
, чтобы найти точки, где 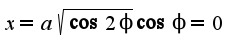
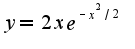
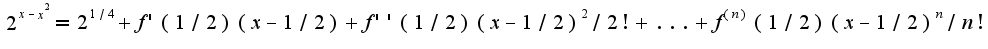 Поэтому надо последовательно находить производные и считать их в точке
Поэтому надо последовательно находить производные и считать их в точке 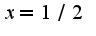 Найдем
Найдем 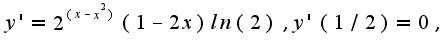
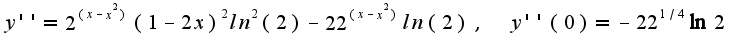
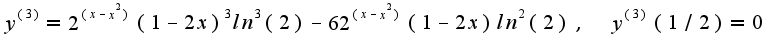
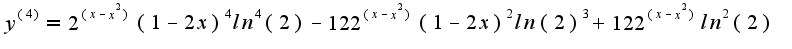
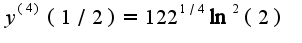 Аналогично,
Аналогично, 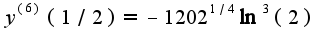
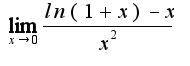 там при разложение все зануляется или неопределенность. можно ли сделать при помощи правила Лопиталя!
там при разложение все зануляется или неопределенность. можно ли сделать при помощи правила Лопиталя!
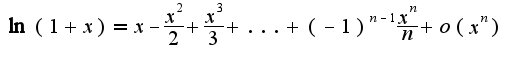 при
при