| Автор | Сообщение |
|---|---|
|
o_a
#
1 дек 2011 |
|
|
paulinio
#
1 дек 2011 |
|
|
paulinio
#
1 дек 2011 |
|
|
o_a
#
1 дек 2011 |
|
|
paulinio
#
4 дек 2011 |
|
|
o_a
#
4 дек 2011 |
|
|
paulinio
#
11 дек 2011 |
|
|
o_a
#
11 дек 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
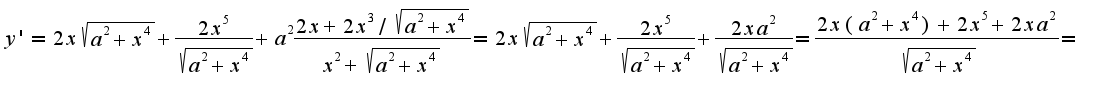
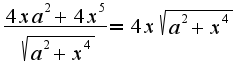
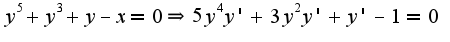 Номер 13.208(2) решается аналогично, точку надо подставить в уравнение, полученное после дифференцирования
Номер 13.208(2) решается аналогично, точку надо подставить в уравнение, полученное после дифференцирования